Multiplication Game
2x, 3x, 4x, 5x & 10x Table – Triarc
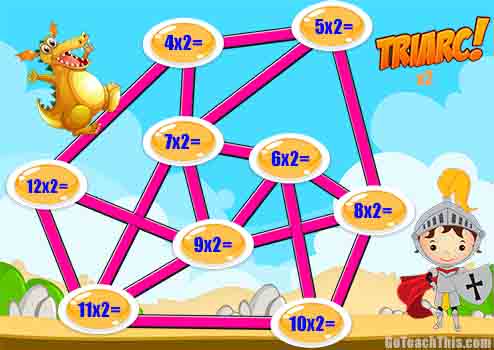
Multiplication Game – Triarc
Multiplication Games – 2x, 3x, 4x, 5x & 10x Table – Triarc:
is a mathematical Three in a Row game that helps students develop strategic thinking, Number Sense & practice Multiplication Facts. Triarc also makes Math lessons a little more enjoyable.
The game is ideal for math groups, math learning centers, tutorial groups or to add a little diversity to your homework program.
What You Need:
1 game board
2 players
5 counters of one color and 5 of another (coins, buttons, very small rocks, pawns from a chess set, etc)
How to Play:
1. The person with the next birthday goes first.
2. Player 1 places a counter on an algorithm, reads it aloud & states the answer.
3. Player 2 checks if the answer given is correct. (If the answer is correct the counter stays, if the answer is incorrect the counter is removed) NB In the case of a ‘stutter’ / self-correction / change of mind etc a class rule will need to be established based on what the class believes will be best for achieving the learning goals of this game.
4. Player 2 then places their counter on a different algorithm and does the same.
5. Players alternate turns aiming to be the first player to get 3 counters in a row along an obtuse angle. The player who gets 3 in a row is declared the winner.
6. The losing player goes first in the next game.
Agreed ‘Extra Rules’ – You will often find extra rules need to be added to ensure the game flows e.g. Does a penalty need to be given if a person, ‘takes too long’ to answer? – If yes, how long is ‘too long’? All extra rules should be made with consideration given to making the learning of math strategies efficient, making the game flow well, and developing a positive attitude to Math.
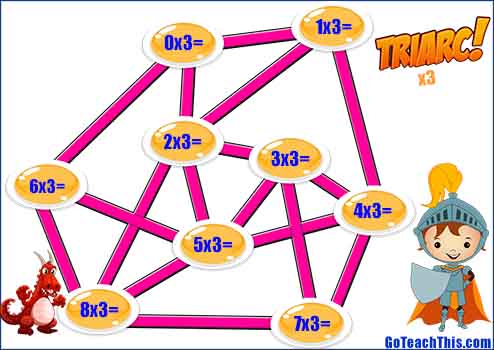
Multiplication Game – Printer Friendly Version
Variation:
Teaching Point – Initially it is good to say the complete algorithm and answer it aloud to aid memorization. However, the game’s main aim is to assist the students to achieve automaticity, so after a while insist on not saying the algorithm and just say the answer.
Before Play Possibilities:
Below are some suggestions to aid the learning. Some questions require students to ‘own’ their feelings so require written responses. NB Confidentiality needs to be assured.
– What does it mean to be truly numerate?
– Explain – ‘Becoming numerate is a progression. You begin counting objects and using numbers. You might then move on to using your fingers to help solve algorithms. Many people get stuck at this point but there are still two stages to go.
Discuss Math Anxiety!
– When was the last time you checked in with your students to see how they feel about Math?
– Write down how you feel when your teacher says, ‘It’s time for Math?’
– What do you think makes you feel this way?
– Does Math make you feel excited? Why or why not? NB ‘I hate it’ or ‘I love it’ is too broad an answer. What do you really ‘love’ or ‘hate’?
– Does Math make you feel inadequate in some way? Why?
– Start looking a little deeper into yourself to find out why you feel this way.
Discuss ‘See It, Say It’
– Confidence with number leads to… (throw it open to the students)
Possibilities for During the Game:
– Tell me how you worked out this algorithm.
– Sit in on a game where students are still silently reciting the whole table until they get to the required answer. Say to them, ‘Try this’ (use a strategy). Invite the students to try it. Did it help? Is it more efficient?
– Take notes on algorithms students ‘stumble’ on and build this into the next lesson.
– Observe the play – keep notes on which students have achieve automaticity.
– Be sure to get around to see the children who have yet to achieve automaticity or are using inefficient strategies.
– How will you differentiate for the students who have achieved automaticity on a given skill?
– What strategy have you developed to give yourself a better chance of winning this game?
– Under stress, people tend to ‘go back’ to what they know. Students often revert to using their fingers to work out answers for certainty. NB There is nothing ‘wrong’ with this strategy as it is accurate, but the problem comes with the strategy being inefficient. What are your thoughts on this? How can we assure all class members move forward with their mental strategies?
– ‘Finger calculations are a natural part of mathematical learning to be worked through, not relied upon for the rest of your life’. ‘What would happen if all the ……….(insert job title)……. used their fingers to solve money problems?
– What mathematical ideas arose during the game you can learn from?
– What different strategy did you find in the game which was efficient and worked?
– What have you achieved in your mathematical thinking today?
Included in this Download:
EXPLORE MORE




