Addition Game – Triarc
22 Addition Game Boards
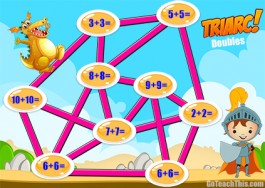
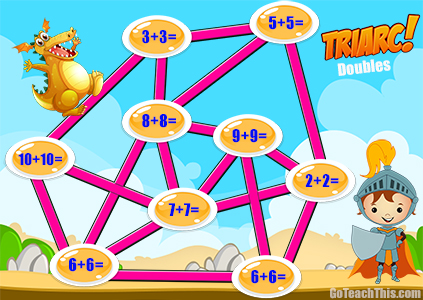
Addition Games – Triarc is a mathematical Three in a Row game that helps students develop strategic thinking, Number Sense & practice Addition Facts. Triarc also makes Math lessons a little more enjoyable.
The game is ideal for Math groups, Math learning centers, tutorial groups or to add a little diversity to your homework program.
Included in this Download:
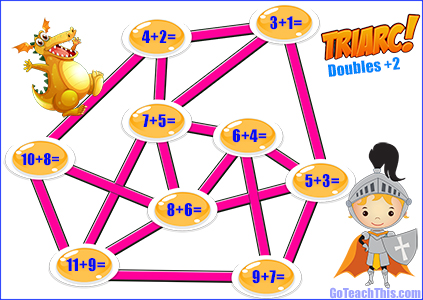
Color AND Low Color Game Boards for Doubles, Doubles Plus One, Doubles Plus Two, Friends to Ten, Friends to 20, Adding 10, Adding 9, Adding 8 & a Blank Board. 22 Game Boards in All PLUS a PowerPoint Version containing all the color game board to aid Number and Strategy Talks.
What You Need:
1 game board
2 players
5 counters of one color and 5 of another (coins, buttons, very small rocks, pawns from a chess set etc)
How to Play:
1. The person with the next birthday goes first.
2. Player 1 places a counter on an algorithm, reads it aloud & states the answer.
3. Player 2 checks if the answer given is correct. (If the answer is correct the counter stays, if the answer is incorrect the counter is removed) NB In the case of a ‘stutter’ / self-correction / change of mind etc a class rule will need to be established based on what the class believes will be best for achieving the learning goals of this game.
4. Player 2 then places their counter on a different algorithm and does the same.
5. Players alternate turns aiming to be the first player to get 3 counters in a row. The player who gets 3 in a row is declared the winner.
6. The losing player goes first on the next game.
Agreed ‘Extra Rules’ – You will often find extra rules need to be added to ensure the game flows e.g Does a penalty need to be given if a person, ‘takes too long’ to answer? – If yes, how long is ‘too long’? All extra rules should be made with consideration given to making the learning of math strategies efficient, making the game flow well & the development of a positive attitude to Math.
Teaching Point – Initially it is good to say the complete algorithm and answer it aloud to aid memorization. However, the game’s main aim is to assist the students to achieve automaticity, so after a while insist on not saying the algorithm and just say the answer.
Before Play Possibilities:
Below are some suggestions to aid the learning. Some questions require students to ‘own’ their feelings so require written responses. NB Confidentiality needs to be assured.
– Discuss and reflect on why we play maths games.
– What does it mean to be truly numerate?
– Explain – ‘Becoming numerate is a progression. You begin counting objects and using numbers. You might then move on to using your fingers to help solve algorithms. Many people get stuck at this point but there are still two stages to go.
– Discuss – The next stage is using strategies to solve algorithms e.g 8+9 is really 8+8+1 = 17 or 9+9-1=. What strategies do you use already in solving algorithms?
– Discuss – The final stage is ‘automaticity’. This means, ‘See It, Say It’. You see the algorithm and you ‘just know’ the answer in your head and can say it without even thinking about it.
– Discuss & Reflect – Some people have automaticity for some facts but not others. Where are you at with your knowledge? How can you identify the algorithms you ‘need to work on’?
– Discuss & Reflect – ‘Depending on the problem you face your strategies to solve it may change’. Think Pair Share what could this mean?
– Discuss & Reflect – ‘Under pressure, people often go back to what they know’. In Math, people may have practiced strategies for weeks but once they have to do a quiz they revert to relying on fingers. People often doubt themselves and go back to what they know is a sure thing. This is a very natural phenomenon that people need to acknowledge in themselves and make efforts to move past. Where are you at in regards to this?
– Discuss – ‘Math games are designed to add just enough pressure to ensure students practice strategies, but not too much so they feel anxious.’ How do you feel when you are playing this game?
– Why do you think games are an effective way to learn basic number facts?
Discuss Math Anxiety!
– What is ‘math anxiety’?
– When was the last time you checked in with your students to see how they feel about Math?
– Write down how you feel when your teacher says, ‘It’s time for Math?’
– What do you think makes you feel this way?
– Does Math make you feel excited? Why or why not? NB ‘I hate it’ or ‘I love it’ is too broad an answer. What do you really ‘love’ or ‘hate’?
– Does Math make you feel inadequate in some way? Why?
– Start looking a little deeper into yourself to find out why you feel this way.
Discuss ‘See It, Say It’
– List 6 reasons why this might be a worthwhile goal.
– Confidence with number leads to… (throw it open to the students)
Possibilities for During the Game:
– Be sure to mention the skill focused on in the game a lot eg if the focus is doubles plus one, ham it up, overuse it, make it a joke, change your tone of voice when you use it, get them to finish your sentence ‘Today we are working on the strategy of ………….’
– Be strategy-focused during play rather than answer-focused.
– Ask, ‘What strategy did you REALLY use to figure out this algorithm?’
– Tell me how you worked out this algorithm.
– Sit in on a game where students are still using their fingers. Say to them, ‘Try this’ (use a strategy). Invite the students to try it. Did it help? Is it more efficient?
– Encourage the students to help each other with learning strategies.
– Take notes on algorithms students ‘stumble’ on and build this into the next lesson.
– Observe the play – keep notes on which students have achieve automaticity.
– Be sure to get around to see the children who have yet to achieve automaticity or are using inefficient strategies.
– What other ‘less efficient’ strategies are the students are using? e.g counting on using a ruler, looking for the number line wall display, etc.
– As a result of your observations design and implement learning experiences that will lead all students towards using strategies and automaticity.
– How will your observations inform your next lesson?
– How will you differentiate for the students who have achieved automaticity on a given skill?
After Game Possibilities: (as a whole class and in pairs reflect)
– What strategies do you need to do well at this game?
– What strategy have you developed to give yourself a better chance of winning this game?
– Under stress people tend to ‘go back’ to what they know. Students often revert to using their fingers to work out answers for certainty. NB There is nothing ‘wrong’ with this strategy as it is accurate, but the problem comes with the strategy being inefficient. What are your thoughts on this? How can we assure all class members move forward with their mental strategies?
– ‘Finger calculations are accurate but not efficient’ ‘How can we do it faster?’
– ‘Finger calculations are a natural part of mathematical learning to be worked through, not relied upon for the rest of your life’. ‘What would happen if all the ……….(insert job title)……. used
their fingers to solve money problems?
– What algorithms do you ‘stumble on’ / balk at? They are the ones you hesitate on or have to think about. Identify them then devise and practice a strategy to help you ‘get better’ at these?
– I’m not ‘bad at maths’ I just use inefficient strategies. What are the effects of seeing yourself as ‘not a Math person’?
– Using inefficient strategies faster is not effective. Trying to use your fingers more quickly will lead to you working really hard and getting anxious about math. Often a whole new way of thinking needs to be developed.
– There is often never one single best way to do a mental computation. As long as it is efficient, accurate and applies in all circumstances it is good’. What could this mean?
– What has changed in your mathematical thinking after today’s maths experience?
– What mathematical ideas arose during the game you can learn from?
– What different strategy did you find in the game which was efficient and worked?
– What have you achieved in your mathematical thinking today?
EXPLORE MORE