Multiplication Game & Division Game
Nine Men’s Morris
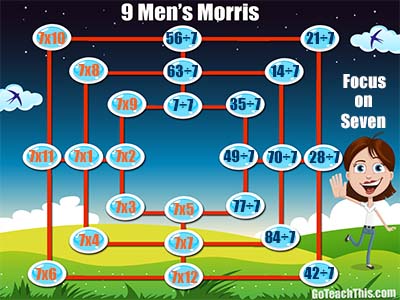
Multiplication & Division Game in One
Nine Men’s Morris:
is a strategy game that most likely originated in the Roman Empire. It is not certain exactly how old the game is as there is conflicting evidence regarding its origin. Estimates on the game’s age vary from about 2 000 to 3 400 years old. This version of the game helps students see the inverse relationship between Multiplication and Division.
Aim:
To develop strategic thinking skills while learning Multiplication & Division Facts and have a little fun doing it.
What you Need:
2 Players
1 Nine Men’s Morris Game Board
9 counters of different colors for each player
How to Play:
1. The game begins with an empty board and each player in possession of 9 counters.
2. The player with the longest hair goes first.
3. Players take turns either:
– placing a counter on an empty space on the board and stating the answer to the algorithm covered aloud to their opponent.
or
– sliding a counter already on the board one space horizontally or vertically along the line to the next empty space. They then read the algorithm landed on to their opponent and answer it aloud.
5. Each time a player gets three of their counters in a row along a single line (this is traditionally called a ‘mill’) they must choose one of their opponent’s counters and remove it from the board. The removed piece takes no further part in the game.
The Two Mill Rule – If by sliding ONE piece TWO MILLs are formed, then TWO of the opponent’s pieces MUST be removed.
Illegal Moves:
1. Diagonal moves are NOT permitted.
2. Placing a piece on top of another is not allowed.
3. A player cannot jump a counter over another counter.
4. Moving a piece in one space and then moving it back to the same space on the next move is also not permitted. NB Even to try this is considered ‘poor form’.
5. Forming a mill, moving a piece out of the mill, and then moving it back on the next turn is illegal.

Multiplication & Division Games
How to Win:
– The player who is left with 2 or fewer pieces on the board loses the game.
Possible Before Game Activities:
– Give students plenty of real-world examples to reinforce the relationship between the abstract and symbolic. Many students know 8 x 5 gives the same answer as 5 x 8, many are unable to represent these in concrete ways. E.g. 5 gardens with 8 rabbits in each is very different from 8 gardens with 5 rabbits in each.
– Use calculators to investigate the inverse relationship between Multiplication and Division. Do some algorithms until the pattern becomes apparent e.g. 5×5=25 so 25÷5=_ and so on.
– When the students get the hang of this have them predict what the answer will be before pressing the equals button.
– Explore both types of division – How many equal groups can be made from 24 with 6 in each group? Share 30 objects between 5 groups. How many in each group. Use real-world examples of this.
During the Game:
– Encourage students to predict what options their opponent has and what moves they may make.
– Have you found any ways to ‘plan ahead’ to help you win the game? Tell me about it.
– Teacher reflects on how to further differentiate this game for future sessions and for which students.

Multiplication PowerPoint Included
Possible after the Game reflections:
– Students draw the difference between 5×3 and 3×5.
– Students draw diagrams and annotate them to show their understanding of 12÷3
– I found it easy/hard to stay focused in math today because_______.
– Today in math I was confused by _______________ so I _________________ to help me understand.
– What did you discover about your use of Division strategies while playing this game.
Included in this Download:
11 Full-Color Game Boards – Multiplication Facts and their Inverse Division Facts – 2 Times Table to Twelve Times Table
1 PowerPoint file with all game boards shown for easy game introduction and number talks.
1 Set of Game Rules
1 Set of Teaching Notes
EXPLORE MORE




